From RankNet to LambdaRank to LambdaMART: An Overview
Published:
微软 2010 年发表的一篇关于 LTR 算法的总结的技术报告.
论文基本信息:
来源:Microsoft Research Technical Report MSR-TR-2010-82, 2010
关键词:learning to rank, RankNet, LambdaRank, LambdaMART
一直没有好好地了解一下搜素里比较经典的那几个算法, 这次借着这篇论文一定好把这些好好搞清楚!
1. Introduction
看文章标题提到了这么多模型, 别慌, 先看看它们之间的关系: LamdaRank 是基于 RankNet 的, LambdaMART 是 LambdaRank 的增强树版本. 这篇技术报告呢, 也就从 RankNet 讲起, 一直推导到 LambdaMART. 当然, 推导过程主要是从算法的损失函数及其梯度出发的.
2. RankNet
RankNet 可以看作一个普通的前馈神经网络, 输入一个样本的特征, 输出是该样本的打分. RankNet 的重点在于其损失函数. 在计算损失函数时, 以同一 query 下相关性不同的 doc 组成 pair, 如 $(x_i, x_j)$. 这一对文档存在一个偏序关系, 我们令 $x_i \triangleright x_j$ (表示 $x_i$ 优于 $x_j$). 那么 RankNet 其实是对这个偏序关系进行预测, 即预测 $P_{ij} = P(x_i \triangleright x_j)$. 令 RankNet 模型为打分函数: $f(\cdot): x \in \mathcal{R}^n \mapsto \mathcal{R}$. 则模型对 $x_i, x_j$ 的打分为 $s_i = f(x_i), s_j = f(x_j)$. 则损失函数为:
\[C = -P_{ij} log \hat{P}_{ij} - (1 - P_{ij} )log (1 - \hat{P}_{ij})\]其中 $P_{ij} \in {0, 1}$, 表示真实的偏序关系, $x_i \triangleright x_j$ 时为 1. $\hat{P}{ij} = \frac{1}{1 + e^{- \sigma (s_i - s_j)}}$, 表示 $x_i \triangleright x_j$ 的概率. 很显然, 上式就是二分类的交叉熵损失函数, 目标变量就是 $0, 1$. 现在来做一个变换, 使其目标变量变为 $-1, 1$. 令 $S{ij} \in {-1, 0, 1}$. $S_{ij} = -1$ 表示 $x_j \triangleright x_i$, $S_{ij} = 1$ 表示 $x_i \triangleright x_j$, $S_{ij} = 0$ 表示 $x_i, x_j$ 的相关性是相同的. 显然, $P_{ij} = \frac{1}{2}(1 + S_{ij})$. 把 $S_{ij}$ 代入 $C$ 中:
\[\begin{aligned} C &= -P \log \hat{P} - (1 - P) \log \frac{e^{-\sigma(s_i-s_j)}}{1 + e^{-\sigma(s_i-s_j)}}\\ &= -P \log \hat{P} - (1 - P) \log (e^{-\sigma(s_i-s_j)} \cdot \hat{P}) \\ &= -P \log \hat{P} - (1 - P) [ -\sigma(s_i - s_j) + \log \hat{P} ] \\ &= -P \log \hat{P} + (1 - P) \sigma(s_i - s_j) - \log \hat{P} + P \log \hat{P} \\ &= (1 - P) \sigma(s_i-s_j) - \log \hat{P} \\ &= (1 - \frac{1}{2}(1 + S)) \sigma(s_i-s_j) - \log \frac{1}{1+e^{-\sigma(s_i-s_j)}} \\ &= \frac{1}{2}(1-S) \sigma(s_i-s_j) + \log (1 + e^{-\sigma(s_i-s_j)}) \\ \end{aligned}\]注意: 上式中省略了下标, 且 $\sigma$ 不是 $sigmoid$ 激活函数, 而是一个系数 (可以对应到 LightGBM 中的 sigmoid 参数).
由于我们只使用相关性等级不同的 doc 组成 pair, 则 $S_{ij}$ 只会等于 -1 或 1. 当 $S_{ij} = 1$ 时, 则:
\[C = \log (1 + e^{-\sigma(s_i-s_j)})\]当 $S_{ij} = -1$ 时:
\[\begin{aligned} C &= \sigma(s_i - s_j) + \log (1 + e^{-\sigma(s_i-s_j)}) \\ &= \log e^{\sigma(s_i - s_j)} + \log (1 + e^{-\sigma(s_i-s_j)}) \\ &= \log [ e^{\sigma(s_i - s_j)} \cdot (1 + e^{-\sigma(s_i-s_j)}) ] \\ &= \log (1+e^{\sigma(s_i - s_j)}) \end{aligned}\]显然, 上述两种情况可以进行统一, 令目标变量为 $y \in {-1, 1}$, 则:
\[C = \log (1 + e^{- y \sigma(s_i-s_j)})\]训练的时候是对同一 query 下的 doc 的偏序关系进行分类, 因此在用 $(x_i, x_j)$ 更新参数 $w$ 时:
\[w \leftarrow w - \eta \frac{\partial C}{\partial w} = w - \eta (\frac{\partial C}{\partial s_i} \frac{\partial s_i}{\partial w} + \frac{\partial C}{\partial s_j} \frac{\partial s_j}{\partial w})\]注意: $\frac{\partial C}{\partial s_i} = - \frac{\partial C}{\partial s_j} = \sigma(\frac{1}{2} (1 - S) - \frac{\sigma}{1 + e^{\sigma (s_i - s_j)}})$. 文中令 $\lambda_{ij} = \frac{\partial C}{\partial s_i}$, 则有:
\[\frac{\partial C}{\partial w} = \lambda_{ij} \frac{\partial s_i}{\partial w}- \lambda_{ij} \frac{\partial s_j}{\partial w} = \lambda_{ij} (\frac{\partial s_i}{\partial w} - \frac{\partial s_j}{\partial w})\]文中还提到了对 RankNet 的一个分解来加速模型的训练. 主要思路就是: 把某个 $x_i$ 与其他 doc 组成的 pair 计算得到的梯度进行累积再一次性进行更新. 令 $I$ 表示同一 query 下的 pair 集. 则利用这个 query 下的 doc 进行参数更新时:
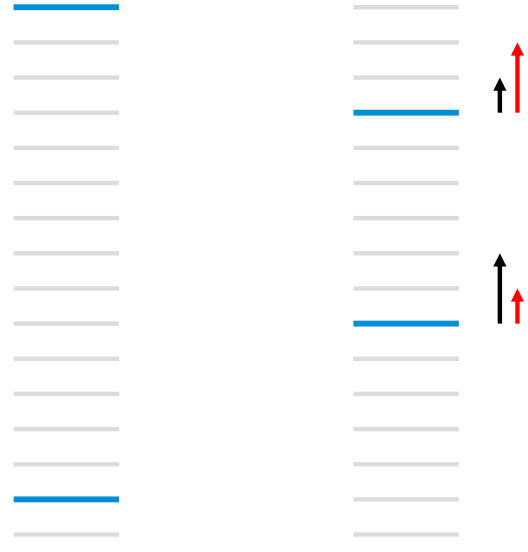
\[\begin{aligned} \frac{C}{\partial w} &= \sum_{(i, j) \in I} (\frac{\partial C}{\partial s_i} \frac{\partial s_i}{\partial w} + \frac{\partial C}{\partial s_j} \frac{\partial s_j}{\partial w}) \\ &= \sum_{(i, j) \in I} \lambda_{ij} \frac{\partial s_i}{\partial w}- \lambda_{ij} \frac{\partial s_j}{\partial w} \\ &= \sum_{(i, j) \in I} \lambda_{ij} (\frac{\partial s_i}{\partial w} - \frac{\partial s_j}{\partial w}) \\ &= \sum_i \lambda_i \frac{\partial s_i}{\partial w} \end{aligned}\]上式中的 $\lambda_i$ 就是 $\lambda$ 梯度, 通过上式也可以看出 $\lambda_i = \sum_{(i, j) \in I} \lambda_{ij} - \sum_{(j, i) \in I} \lambda_{ji}$. $\lambda_i$ 的含义就是: $x_i$ 排在前的 pair 的梯度和减去 $x_i$ 排在后的 pair 的梯度和. 如下图所示, 红色的箭头就是 $\lambda_i$.
有序文档列表 所示.
3. Information Retrieval Measures
常用的指标: MAP (Mean Average Precision), MRR (Mean Reciprocal Rank), ERR (Expected Reciprocal Rank), NDCG (Normalized Discounted Cumulative Gain) 等.
4. LambdaRank
LambdaRank 在 RankNet 的基础上, 在 $\lambda_{ij}$ 的基础上乘以了 $i, j$ 交换时观测指标的变化量 $\Delta Z_{ij}$, 其中 $Z$ 可以是 NDCG 或者 MAP 等.
5. LambdaMART
LambdaMART 结合了 MART (Multiple Additive Regression Tree) 和 LambdaRank. 简单来说就是将 $\lambda$ 梯度与 GBDT 结合. 以 LightGBM 为例, 定义新的损失时只需要定义样本的一阶, 二阶导即可, 就可进行树的学习 (结点分裂, 叶子节点分数的计算).
