Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba
Published:
阿里淘宝团队 18 年在 KDD 上发表的一篇结合 side information 生成结点表征的论文. 通常用于做召回, 解决物品冷启动问题.
论文基本信息:
来源:阿里淘宝, 香港科技大学
关键词:Recommender systems; Graph Embedding; Item Similarity
1. Introduction
主要是为了解决淘宝的推荐中的三个问题:
Scalability. 现有的推荐方法在百万级别的数据集上工作良好, 但在十亿级别的数据集上却效果不佳. 淘宝中的用户和物品都在十亿级别, 如何在如此大规模的数据上做推荐是一个很有挑战的问题;
Sparsity. 由于用户倾向于与一小部分物品产生交互 — 数据的稀疏性. 传统 CF (Collaborative Filtering) 容易受到数据稀疏性的影响. 如何为这种交互行为少的用户或长尾物品做推荐?
Cold Start. 在淘宝中, 每小时都有上百万的新增物品, 新增物品是没有交互记录的, 很难预测用户是否对这些新物品感兴趣.
为了解决以上问题, 淘宝设计了一个两阶段的推荐框架: 1) 匹配阶段. 根据用户的行为, 生成一个与历史交互相似的物品集合; 2) 排序. 根据用户的偏好, 训练一个深度模型对候选集的物品进行排序. 改论文研究的是匹配阶段的问题, 该阶段的核心问题就是 如何基于用户行为计算物品之间的相似性.
2. Preliminaries
论文的目的就是得到每个物品的表征, 用于计算物品的相似性, 方便做召回. 其中有几个关键之处:
- 如何构建图;
- 如何利用 side information;
- 如何学习结点的的表征;
3. How To Do
3.1. Construction of Item Graph from Users’ Behaviors
传统的 CF 不仅会受到数据稀疏性的影响, 而且会忽略用户行为中隐含的序列信息. 建图的思路也比较直接, 以物品为结点, 相邻的物品之间存在边, 构建有向带权图. 建图的大致流程:
- 对用户行为进行过滤. 过滤的情况:
- 点击后停留的时间小于 1 秒的物品, 应被去除;
- 过滤刷单用户 (spam user) 的行为. spam user 的特征: 在不到三个月的时间里买了超过 1000 个商品或者点击次数超过 3500;
- 店家经常会更新商品的信息, 极端的情况下一个物品可以完全变成另外一个物品. 这种变化很大的物品也需要移除;
- 按照时间窗口将用户的行为划分成 sessions. 时间窗口的大小一般是一个小时. 如 Construct Graph(a) 所示, U2 的行为序列被分成了 BE 和 DEF 两部分.
- 构建 item graph. 计算边的权重. 边 $e_{ij}$ 的权重等于在所有的 sessions 中, $i \rightarrow j$ 的次数.
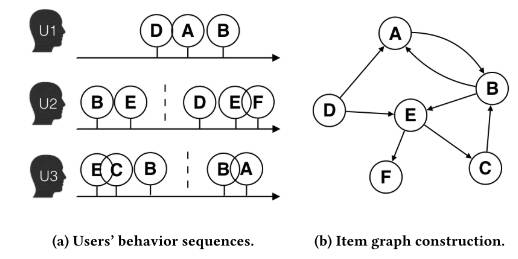
3.2. Base Graph Embedding
在得到 Item graph 后就是解决怎么得到物品表征的问题了. 令 Item graph 为 $\mathcal{G}(\mathcal{V}, \mathcal{E})$, $M$ 为邻接矩阵, $M_{ij}$ 表示由 $i \rightarrow j$ 的权重, 为上一步计算的权重的归一化值:
\[P\left(v_j \mid v_i\right)= \begin{cases} \frac{\mathrm{M}_{i j}}{\sum_{j \in N_{+}\left(v_i\right)} \mathrm{M}_{i j}}, & v_j \in N_{+}\left(v_i\right) \\ 0, & e_{i j} \notin \mathcal{E} \end{cases}\]其中 $N_+(v_i)$ 表示结点 $v_i$ 的出边邻居.
学习结点表征的方式和 Deepwalk 类似, 也是先进行随机游走, 然后应用 Word2vec 的 Skip-gram 算法来学习结点的表征. 因此, 为了得到结点表征, 等价于求解如下优化问题:
\[\underset{\Phi}{\operatorname{minimize}}-\log \operatorname{Pr}\left(\left\{v_{i-w}, \cdots, v_{i+w}\right\} \backslash v_i \mid \Phi\left(v_i\right)\right)\]其中 $\Phi: \mathcal{V} \mapsto \mathbb{R}^d$ 表示结点的表征, $w$ 表示 Skip-gram 中窗口的大小. 基于独立性的假设, 有:
\[\operatorname{Pr}\left(\left\{v_{i-w}, \cdots, v_{i+w}\right\} \backslash v_i \mid \Phi\left(v_i\right)\right)=\prod_{j=i-w, j \neq i}^{i+w} \operatorname{Pr}\left(v_j \mid \Phi\left(v_i\right)\right)\]注意, 上式中只有正样本, 为了使用梯度下降法来学习, 一般会进行负采样, 因此最终的优化问题转化为:
\[\underset{\Phi}{\operatorname{minimize}} \log \sigma\left(\Phi\left(v_j\right)^T \Phi\left(v_i\right)\right)+\sum_{t \in N\left(v_i\right)^{\prime}} \log \sigma\left(-\Phi\left(v_t\right)^T \Phi\left(v_i\right)\right)\]其中 $N(v_i)^\prime$ 是为 $v_i$ 采样得到的负样本集合, $\sigma(\cdot)$ 是 sigmoid 函数. 这一步的过程如 Base Graph Embedding 所示.
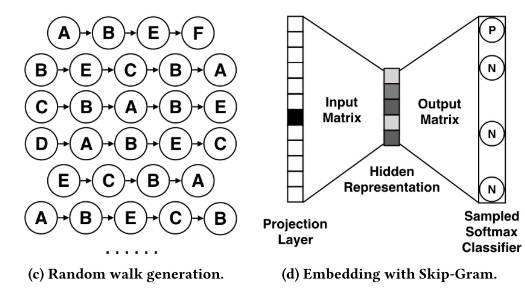
3.3. Graph Embedding with Side Information
上述只是很基本的表征学习方法, 只利用了用户的行为序列信息, 不利于新增物品或者长尾物品的推荐. 通过 side information , 如物品的属性等, 可以缓解冷启动带来的问题. 论文中提出了 GES (Graph Embedding with Side information) 来将 side information 融入近物品的表征中.
定义 $W$ 为物品本身的 embedding 矩阵和 side information 的 embedding 矩阵. $W_v^0$ 为 $v$ 的本身的表针 (即不使用 side information 时通过 Skip-gram 学习到的表征), $W_v^s$ 为 $v$ 的第 $s$ 种 side information 的表征. 因此, 对 $v$ 来说一共有 $n+1$ 种表征, 分别为 $W_v^0, W_v^1, \cdots, W_v^n \in \mathbb{R}^d$. 为了得到最终物品的表征 $H_v$, GES 种使用了 avg pooling 来进行聚合:
\[H_v = \frac{1}{n+1} \sum_{s=0}^n W_v^s\]至此, 通过 Skip-gram 学习到的表征以及 side information 就融合起来了! 但是 side information 的表征从何而来呢? 如 Framework 所示. side information 一般是稀疏特征, 其 embedding 也是通过学习得到的. 学习的任务即 Skip-gram 中的任务, 由中心词即其 context 构成正样本, 负采样得到负样本. Skip-gram 训练完后就得了结点本身的表征以及 side information 的表征. 其实 side information 的就是特征的 embedding, 这与后期的 Embedding&MLP 的结构基本一致.
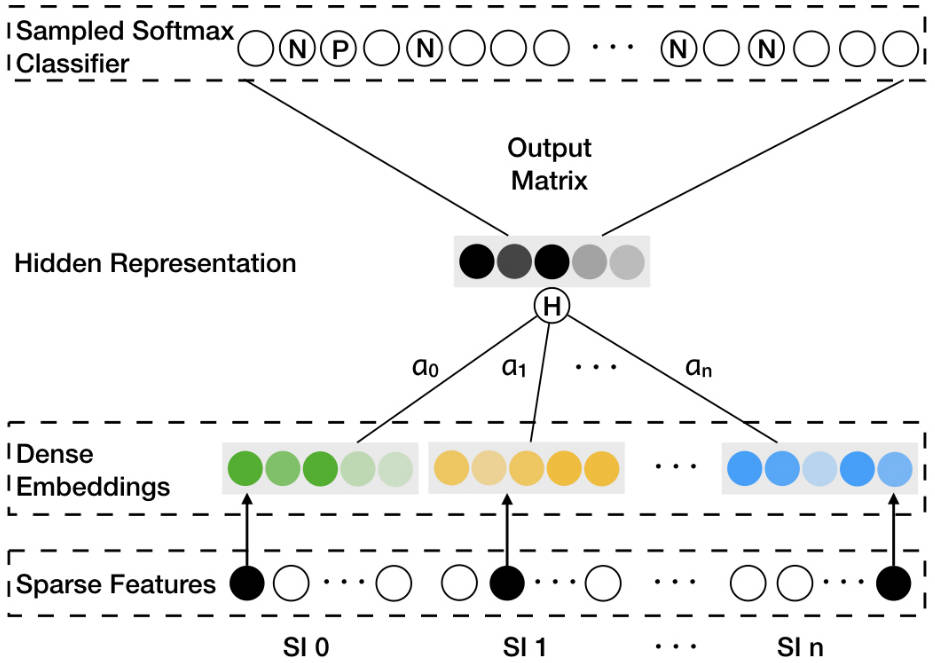
3.4. Enhanced Graph Embedding with Side Information
GES 只是对 side information 进行了简单的平均, 但是不同的 side information 的重要性显然是不一样的 — 在不同的物品中, side information 的重要性也是不一样的. 这就呼之欲出了, 我们需要一个权重(换个时髦点的说法, attention-mechanism). 定义权重矩阵 $A \in \mathbb{R}^{|V| \times (n+1)}$, $A_{ij}$ 表示的是第 $j$ 个 side information 对物品 $i$ 的重要性, 其中 $A_{*0}$ 表示物品本身的表征的重要性. 文中使用 $a_v^j$ 来表示 $A_{vj}$. 那么物品最终的表征即:
\[H_v = \frac{\sum_{j=0}^n e^{a_v^j} W_v^j}{\sum_{j=0}^n e_v^j}\]至此, EGES 的框架就差不多完了. 其实简单而言就是构建好 Item graph 后, 以 Skip-gram 的方式学习表征 $W^0, \cdots, W^n$ 和 权重矩阵 $A$. 学习的任务也和 Skip-gram 中是一致的. 后续如果要使用的话就可以直接拿到物品本身的 embedding 和 对应的 side information 的表征了. 对于新增物品, 则可以直接把对应的 side information 表征取出来作为其表征来做召回了. 感觉和 FM 做召回有点类似😄
4. Conclusion
Word2vec 是 2013 年的, Deepwalk 是 2014 年的, 这篇论文是 2018 年的, 还有个 Node2vec 是 2016 年的, Item2vec 也是 2016 年的. 其实纵观这几中方法, 都是以 Word2vec 为基础的, 生成游走序列, 然后一般用 Skip-gram 进行学习.
EGES 中其实也体现了这一变化:
- 最基础版本的 BGE 与 Deepwalk 并没有很大差别;
- GES 则以 avg pooling 的形式融合了 side information, 并在 Skip-gram 学习的过程中学习 side information 的表征;
- 加权的形式融合表征, 且权重通过学习得到.
